5. Графическое изображение  статистических данных

5.1. Понятие о статистическом графике. Элементы статистического графика

Современный анализ социально-экономических явлений немыс­лим без применения графического метода представления данных.

Графический метод есть метод условных изображений статисти­ческих данных при помощи геометрических фигур, линий, точек и разнообразных символических образов.

Главное достоинство статистических графиков - наглядность. При правильном их построении статистические показатели привлекают к себе внимание, становятся более понятными, выразительными, лако­ничными, запоминающимися. Графики прочно вошли в практическую работу экономистов, статистиков и работников учета. В ряде случаев графики стали незаменимым средством обобщения статистических данных, подведения итогов сложных исследований и выявления связи между явлениями. Поэтому необходимо уметь строить и читать стати­стические графики.

Для построения графика необходимо определить, для каких це­лей он составляется, и тщательно изучить исходный материал. Но самое главное условие - это овладение методологией графических изображений. В статистическом графике различают следующие ос­новные элементы: графический образ; поле графика; пространствен­ные ориентиры, масштабные ориентиры; экспликации графика.

Рассмотрим подробнее каждый из указанных элементов.

Графический образ - это символические знаки, с помощью кото­рых изображаются статистические данные: линии, точки, плоские геометрические фигуры (прямоугольники, квадраты, круги и т.д.

В качестве графического образа выступают и объемные фигуры. Иног­да в графиках используются и негеометрические фигуры в виде силу­этов или рисунков предметов.

Одни и те же статистические данные можно изобразить с помо­щью различных графических образов. Поэтому при построении гра­фика важен правильный подбор графического образа. Он должен до­ходчиво отображать изучаемые показатели и соответствовать основному предназначению графика.

Полем графика является место, на котором он выполняется. Это листы бумаги, географические карты, план местности и т.п. Поле гра­фика характеризуется его форматом (размерами и пропорциями сто­рон). Размер поля графика зависит от его назначения. Стороны поля статистического графика обычно находятся в определенной пропор­ции. Принято считать, что наиболее оптимальным для зрительного восприятия является график, выполненный на поле прямоугольной формы с соотношением сторон 1:1,3 до 1:1,5; этот вариант именуется правилом «золотого сечения». Иногда используется и поле графика с равными сторонами, т.е. в виде квадрата.

Построение графика - это всегда творческий процесс. Здесь не­обходим некоторый поиск. Лишь после составления и сравнения не­скольких черновых вариантов можно определить правильную компо­зицию графика, установить масштабы и расположение знаков на поле графика.

Пространственные ориентиры графика задаются в виде систе­мы координатных сеток. Система координат необходима для разме­щения геометрических знаков в поле графика. Наиболее распростра­ненной является система прямоугольных координат. Для построения статистических графиков используется обычно только 1-й и изредка 1-й и 4-й квадраты. В практике графического изображения применя­ются также полярные координаты. Они необходимы для наглядного изображения циклического движения явления во времени. В поляр­ной системе координат (рис. 5.1.а) один из лучей, обычно правый гори­зонтальный, принимается за ось ординат, относительно которой оп­ределяется угол луча (первая координата). Второй координатой считается ее расстояние от центра сетки, называемое радиусом.

 

 

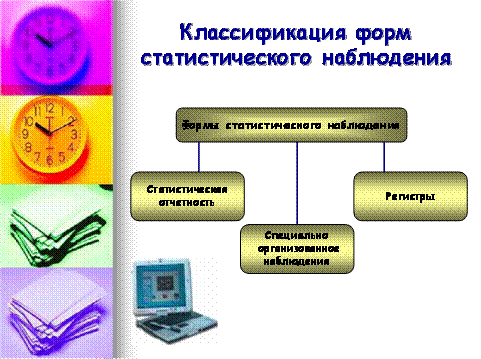
Рис. 5.1. 

 В радиальных графиках лучи обозначают моменты времени, а окруж­ность - величину изучаемого явления. На статистических картах про­странственные ориентиры задаются контурной сеткой (контуры рек, береговая линия морей и океанов, границы государств) и определяют те территории, к которым относятся статистические величины.

Масштабные ориентиры статистического графика определяют­ся масштабом и системой масштабных шкал. Масштаб статистичес­кого графика - это мера перевода числовой величины в графическую.

Масштабной шкалой называется линия, отдельные точки которой могут быть прочитаны как определенные числа. Шкала имеет большое значение в графике и включает три элемента: линию (или носитель шкалы); определенное число помеченных черточками точек, которые расположены на носителе шкалы в определенном порядке, цифровое обозначение чисел, соответствующих отдельным помеченным точкам. Как правило, цифровым обозначением снабжаются не все помеченные точки, а лишь некоторые из них, расположенные в определенном по­рядке. По правилам числовое значение необходимо помещать строго против соответствующих точек, а не между ними (рис. 5.1,б).

Носитель шкалы может представлять собой как прямую, так и кривую линии. Поэтому различают шкалы прямолинейные (например, миллиметровая линейка) и криволинейные - дуговые и круговые (ци­ферблат часов).

Графические и числовые интервалы бывают равными и неравными. Если на всем протяжении шкалы равным графическим интервалам со­ответствуют равные числовые, такая шкала называется равномерной. Когда же равным числовым интервалам соответствуют неравные графические интервалы, и наоборот, шкала называется неравномерной.

Масштабом равномерной шкалы называется длина отрезка (гра­фический интервал), принятого за единицу и измеренного в каких-либо мерах. Чем меньше масштаб (рис. 5.2), тем гуще располагаются на шкале точки, имеющие одно и то же значение. Построить шкалу — это значит на заданном носителе шкалы разместить точки и обозна­чить их соответствующими числами согласно условиям задачи. Как правило, масштаб определяется примерной прикидкой воз­можной длины шкалы и ее пределов. Например, на поле в 20 клеток надо построить шкалу от 0 до 850. Так как 850 не делится удобно на 20, то округляем число 850 до ближайшего удобного числа, в данном случае 1000 (1000 : 20 = 50), т.е. в одной клетке 50, а в двух клетках 100; следовательно, масштаб - 100 в двух клетках.

Рис. 5.2. Масштабы

 

Из неравномерных шкал наибольшее распространение имеет ло­гарифмическая. Методика ее построения несколько иная, так как на этой шкале отрезки пропорциональны не изображаемым величинам, а их логарифмам. Так, при основании 10  lg1 = 0; lg10 = 1; lg100 = 2 и т.д. (рис. 5.3).

Рис. 5.3. Шкалы

 

Последний элемент графика - экспликация. Каждый график должен иметь словесное описание его содержания. Описание включает название графика, которое в краткой форме передает его содержание надписи вдоль масштабных шкал и пояснения к отдельным частям графика.

5.2. Классификация видов графиков

Существует множество видов графических изображений (рис. 5.4 и 5.5).

Их классификация основана на ряде признаков, в основе которых

• способ построения графического образа;
• геометрические знаки, изображающие статистические показатели;
• задачи, решаемые с помощью графического изображения.

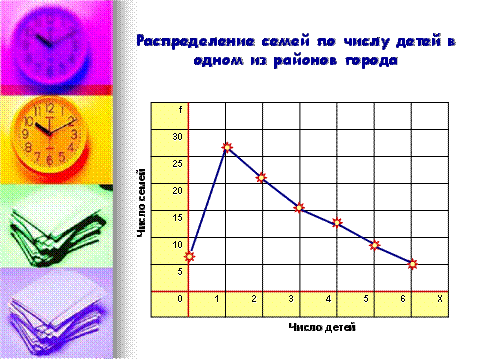
Рис. 5.4.

По способу построения статистические графики делятся на диаг­раммы и статистические карты.

Диаграммы - наиболее распространенный способ графических изображений. Это графики количественных отношений. Виды и спо­собы их построения разнообразны. Применяются диаграммы для на­глядного сопоставления в различных аспектах (пространственном, временном и др.) независимых друг от друга совокупностей. При этом сравнение исследуемых совокупностей производится по какому-либо существенному варьирующему признаку.

Статистические карты - графики количественного распреде­ления по конкретной территории. По своей основной характеристике эти графики близко примыкают к диаграммам и специфичны лишь в том отношении, что представляют собой условные изображения ста­тистических данных на контурной географической карте. Их задачи -отражать пространственное размещение или пространственную рас­пространенность статистических данных. Статистические карты по графическому образу делятся на картограммы и картодиаграммы.

Геометрические знаки, как было сказано выше, представляют со­бой точки, либо линии или плоскости, либо геометрические фигуры. В соответствии с этим различают графики точечные, линейные, плос­костные и пространственные (объемные).

При построении точечных диаграмм в качестве графических об­разов применяются совокупности точек; при построении линейных - линии. Основной принцип построения всех плоскостных диаграмм сводится к тому, что статистические показатели изображаются в виде геометрических фигур и, в свою очередь, подразделяются на столби­ковые, полосовые, круговые, квадратные и фигурные.

В зависимости от круга решаемых задач выделяют диаграммы сравнения, структурные диаграммы и диаграммы динамики.

Особым видом графиков являются диаграммы распределения ве­личин, представленных вариационным рядом, - гистограмма, поли­гон, огива, кумулята.

 

5.3. Диаграммы сравнения

Наиболее распространенными диаграммами сравнения являются столбиковые диаграммы. Это графическое изображение статистичес­ких показателей в виде столбиков-прямоугольников. Данные диаграм­мы широко используются для наглядного сравнения объектов изучае­мых явлений во времени и пространстве, а также для изображения структуры явлений.

При построении столбиковых диаграмм необходимо начертить систему прямоугольных координат, в которой расположатся столби­ки. На горизонтальной оси располагают основания столбиков, раз­мер основания столбиков определяется произвольно, но должен быть одинаковым для всех.

Для построения диаграммы (рис. 5.6) берем систему прямоуголь­ных координат. На оси абсцисс на одинаковом расстоянии друг от друга наносим шесть отрезков равной длины - основания для стол­биков. Высота столбиков определяется в соответствии с принятым масштабом по оси ординат и значениями показателей. Учитывая раз­мер поля графика и максимальное значение показателя, установим масштаб.

Наглядность данной диаграммы достигается сравнением высоты столбиков.

Размещение столбиков в поле графика может быть различным

• на одинаковом расстоянии друг от друга;
• вплотную друг к другу;
• в частичном наложении друг на друга.

Столбиковые диаграммы целесообразно применять для сравне­ния нескольких показателей.

Разновидность столбиковых диаграмм составляют так называе­мые ленточные, или полосовые, диаграммы. Их отличие состоит в том, что масштабная шкала расположена по горизонтали сверху или снизу и она определяет величину полос по длине.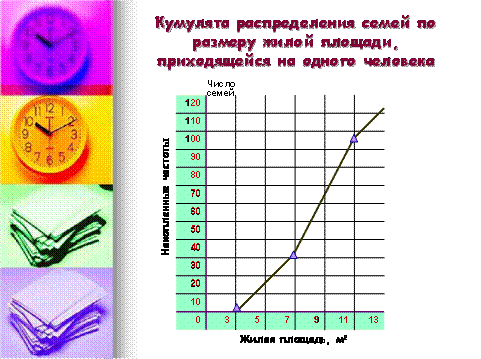Рис. 5.6.

 Столбиковые и полосовые диаграммы хорошо подходят для харак­теристики состава совокупности. Структура состава совокупности луч­ше воспринимается не в абсолютных, а в относительных величинах. При таких данных все столбики (полосы) в диаграмме имеют одинако­вую высоту и соответствуют 100%. Каждый столбик разбивается на части пропорционально удельному весу отдельных частей во всей со­вокупности.

Таким образом, область применения столбиковых и полосовых диаграмм одинакова, так как идентичны правила их построения. Од­номерность изображаемых статистических показателей и их одномасштабность для различных столбиков и полос требуют выполнения единственного положения: соблюдения соразмерности (столбиков - по высоте, полос - по длине) и пропорциональности изображаемым величинам.

Для выполнения этого требования необходимо соблюдать следу­ющие условия:

• шкала, по которой устанавливается размер столбика (полосы),
  должна начинаться с нуля;
• шкала должна быть непрерывной, т.е. охватывать все числа данного статистического ряда;
• разрыв шкалы и соответственно столбиков (полос) не допускается.

Невыполнение указанных правил приводит к искаженному графи­ческому представлению анализируемого статистического материала.

Разновидностью столбиковых (ленточных) диаграмм являются на­правленные диаграммы. Они отличаются от обычных двусторонним расположением столбиков или полос и имеют начало отсчета по масш­табу в середине. Обычно такие диаграммы применяются для изображения величин противоположного качественного значения. Сравнение между собой столбиков (полос), направленных в разные стороны, ме­нее эффективно, чем расположенных рядом в одном направлении. Не­смотря на это, анализ направленных диаграмм позволяет делать доста­точно содержательные выводы, так как особое расположение придает графику яркое изображение. К группе двусторонних относятся диаг­раммы числовых отклонений. В них полосы направлены в обе сторо­ны от вертикальной нулевой линии: вправо - для прироста; влево - для уменьшения. С помощью таких диаграмм удобно изображать отклоне­ния от плана или некоторого уровня, принятого за базу сравнения. Важ­ным достоинством рассматриваемых диаграмм является возможность видеть размах колебаний изучаемого статистического признака, что само по себе имеет большое значение для экономического анализа. Данные диаграммы широко применяются в демографии.

Для простого сравнения независимых друг от друга показателей могут также использоваться диаграммы, принцип построения кото­рых состоит в том, что сравниваемые величины изображаются в виде правильных геометрических фигур, которые строятся так, чтобы пло­щади их относились между собой как количества, этими фигурами изображаемые. Иными словами, эти диаграммы величину изобража­емого явления выражают размером своей площади.

Для создания диаграмм такого типа используют разнообразные геометрические фигуры - квадраты, круги, реже – прямоугольники (рис. 5.7).

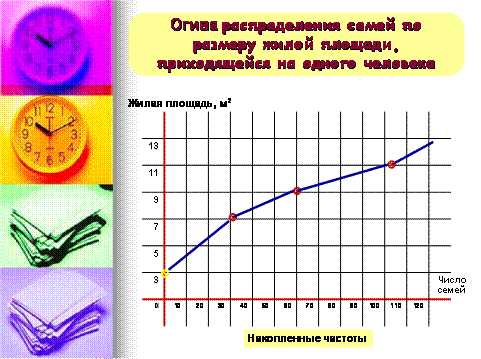
Рис. 5.7.

Для построения квадратных и круговых диаграмм необходимо сначала из статистических данных извлечь квадратные корни. Затем на базе полученных результатов определить сторону квадрата или ради­ус круга в соответствии с принятым масштабом.

Для правильного построения диаграмм квадраты или круги необ­ходимо расположить на одинаковом расстоянии друг от друга, а в каж­дой фигуре указать числовое значение, которое она изображает, не приводя масштаба измерения.

К рассматриваемому виду диаграмм относится графическое изоб­ражение, полученное путем построения один в другом квадратов, кру­гов или прямоугольников с различной заштриховкой или закраской. Такие диаграммы также позволяют сравнивать между собой ряд ис­следуемых величин.

Прямоугольные диаграммы (не квадраты) находят себе применение - при графическом изображении, главным образом для двумасштабных сравнений: один масштаб для основания, другой - для высоты. Эти ди­аграммы называются знаками Варзара. Обычно они применяются в тех случаях, когда показатель является произведением двух других (напри­мер, сумма вкладов есть произведение числа вкладов на средний размер вкладов; численность населения является произведением плотности на­селения на территорию; валовой сбор есть произведение посевной пло­щади на урожайность и т.д.). Такой показатель можно графически изоб­разить в виде сомножителей. Для этого поступают следующим образом: один сомножитель принимают за основание, другой - за высоту. Затем устанавливают масштабы: один для основания, другой для высоты. Да­лее, располагая значением показателя основания и высоты, строят пря­моугольники.

Весьма выразителен и хорошо воспринимается способ построения диаграмм сравнения в виде фигур-знаков. В этом случае статистичес­кие показатели изображаются не геометрическими фигурами, а симво­лами или знаками, воспроизводящими в какой-то степени внешний образ статистических данных. Достоинство такого способа графичес­кого изображения заключается в высокой степени наглядности, в полу­чении подобного отображения, отражающего содержание сравнивае­мых совокупностей.

Важнейший признак любой диаграммы - масштаб. Поэтому, что­бы правильно построить фигурную диаграмму, необходимо опреде­лить единицу счета. В качестве последней принимается отдельная фигура (символ), которой условно присваивается конкретное численное значение. А исследуемая статистическая величина изображается отдельным количеством одинаковых по размеру фигур, последова­тельно располагающихся на рисунке. Однако в большинстве случаев не удается изобразить статистический показатель целым количеством фигур. Последнюю из них приходится делить на части, так как по масштабу один знак является слишком крупной единицей измерения. Обычно эта часть определяется на глаз. Сложность точного ее опре­деления является недостатком фигурных диаграмм. Однако если боль­шая точность представления статистических данных не преследует­ся, то результаты получаются вполне удовлетворительными.

Пример. Рассмотрим построение фигурной диаграммы по дан­ным закупок крупного рогатого скота в одном из регионов России в хозяйствах всех категорий.

В 1999 г. - 6,5 млн т, в 2000 г. - 4,4 млн т, в 2001 г. - 33 млн т.

Примем условно за один знак 1,1 млн т закупок крупного рогатого скота. Разделим приведенные показатели на 1,1 и получим число фи­гур: для 1999 г. - 6; для 2000 г. - 4; для 2001 г. - 3. Построим диаграмму (рис.5.8).

Рис. 5.8.  Динамика закупок крупного рогатого скота в одном

из регионов РФ в хозяйствах всех категорий (в весе живого скота)

за 1999-2001 гг.

 

5.4. Структурные диаграммы

Основное назначение структурных диаграмм заключается в на­глядной иллюстрации структуры какого-либо явления, характеристи­ке удельных весов отдельных частей целого, выявлении структур­ных сдвигов.

В качестве графического образа для изображения структуры со­вокупностей применяются прямоугольники - для построения стол­биковых и полосовых диаграмм и круги - для построения секторных диаграмм.

Круг часто используется в качестве геометрической формы при построении диаграммы. Следует различать два вида применения кру­га. В одном случае сравниваются площади кругов друг с другом. Та­кого рода диаграмма называется круговой (рис. 5.9). В другом случае круг используется для сравнения площади отдельных секто­ров друг с другом. Такая диаграмма именуется секторной.

На этом рисунке каждая из полос диаграммы будет иметь одина­ковую длину, так как в относительных величинах погасятся различия абсолютных размеров совокупностей. В то же время структурные различия проявятся значительно четче. Построение секторной диаграммы начинается с определения цен­тральных углов секторов.

Применение секторных диаграмм позволяет графически не толь­ко изобразить структуру совокупности и ее изменение, но и показать динамику численности этой совокупности.

Рассмотренные способы графического изображения структуры совокупности имеют как достоинства, так и недостатки.

Так, секторная диаграмма сохраняет наглядность и выразитель­ность лишь при небольшом числе частей совокупности, в противном случае ее применение малоэффективно. Кроме того, наглядность сек­торной диаграммы снижается при незначительных изменениях струк­туры изображаемых совокупностей: она выше, если имеются существенные различия сравниваемых структур. Преимуществом столби­ковых (ленточных) структурных диаграмм по сравнению с секторны­ми являются их большая емкость, возможность отразить более широ­кий объем полезной информации.

Рис. 5.9.

 

5.5. Диаграммы динамики

Для изображения и внесения суждений о развитии явления во времени строятся диаграммы динамики.

Для наглядного изображения явлений в рядах динамики исполь­зуются диаграммы: столбиковые, ленточные, квадратные, круговые, линейные, радиальные и др. Выбор вида диаграммы зависит в основ­ном от особенностей исходных данных, цели исследования. Напри­мер, если имеется рад динамики с несколькими неравноотстоящими уровнями во времени (1913, 1940, 1950, 1980, 1985, 2002гг.), то часто для наглядности используют столбиковые, квадратные или круговые диаграммы. Они зрительно впечатляют, хорошо запоминаются, но не годны для изображения большого числа уровней, так как громоздки. Когда число уровней в ряду динамики велико, целесообразно приме­нять линейные диаграммы, которые воспроизводят непрерывность процесса развития в виде непрерывной ломаной линии. Кроме того, линейные диаграммы удобно использовать, если целью исследова­ния является изображение общей тенденции и характера развития явления; когда на одном графике необходимо изобразить несколько динамических рядов с целью их сравнения; если наиболее существен­ным является сопоставление темпов роста, а не уровней.

Для построения линейных графиков применяют систему прямоу­гольных координат. Обычно по оси абсцисс откладывают время (годы, месяцы и т.д. ), а по оси ординат - размеры изображаемых явлений или процессов. На оси ординат наносят масштабы. Особое внимание следует обратить на их выбор, так как от этого зависит общий вид графика. Обеспечение равновесия, пропорциональности между ося­ми координат необходимо в графике потому, что нарушение равнове­сия между осями координат дает неправильное изображение разви­тия явления. Если масштаб для шкалы на оси абсцисс очень растянут по сравнению с масштабом на оси ординат, то колебания в динамике явления мало выделяются, и, наоборот, преувеличение масштаба по оси ординат по сравнению с масштабом на оси абсцисс дает резкие колебания. Равным периодам времени и размерам уровня должны со­ответствовать равные отрезки масштабной шкалы.

В статистической практике чаще всего применяются графичес­кие изображения с равномерными шкалами. По оси абсцисс они бе­рутся пропорционально числу периодов времени, а по оси ординат - пропорционально самим уровням. Масштабом равномерной шкалы будет длина отрезка, принятого за единицу (рис. 5.10).

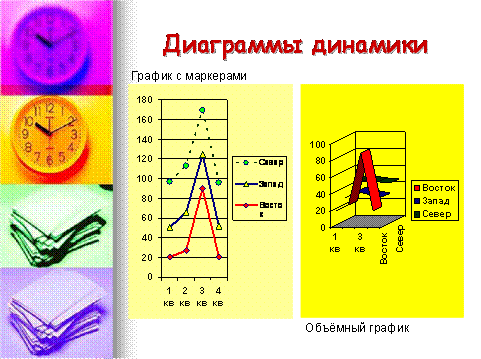
Рис. 5.10.

 

Нередко на одном линейном графике приводится несколько кри­вых, которые дают сравнительную характеристику динамики различ­ных показателей или одного и того же показателя.

Однако на одном графике не следует помещать более трех-четы­рех кривых, так как большое их количество неизбежно осложняет чертеж и линейная диаграмма теряет наглядность.

В некоторых случаях нанесения на один график двух кривых дает возможность одновременно изобразить динамику третьего показате­ля, если он является разностью первых двух. Например, при изобра­жении динамики рождаемости и смертности площадь между двумя кривыми показывает величину естественного прироста или естествен­ной убыли населения.

Иногда необходимо сравнить на графике динамику двух показате­лей, имеющих различные единицы измерения. В таких случаях пона­добится не одна, а две масштабные шкалы. Одну из них размещают справа, другую - слева. Однако такое сравнение кривых не дает доста­точно полной картины динамики этих показателей, так как масштабы произвольны. Поэтому сравнение динамики уровня двух разнородных показателей следует осуществлять на основе использования одного масштаба после преобразования абсолютных величин в относительные.

Линейные диаграммы с равномерной шкалой имеют один недо­статок, снижающий их познавательную ценность: равномерная шка­ла позволяет измерять и сравнивать только отраженные на диаграмме абсолютные приросты или уменьшения показателей на протяжении исследуемого периода. Однако при изучении динамики важно знать относительные изменения исследуемых показателей по сравне­нию с достигнутым уровнем или темпы их изменения. Именно отно­сительные изменения экономических показателей в динамике иска­жаются при их изображении на координатной диаграмме с равномерной вертикальной шкалой. Кроме того, в обычных коорди­натах теряет всякую наглядность изображение для рядов динамики с резко изменяющимися уровнями, которые обычно имеют место в ди­намических рядах за длительный период времени.

В этих случаях следует отказаться от равномерной шкалы и поло­жить в основу графика полулогарифмическую систему. Основная идея полулогарифмической системы состоит в том, что в ней равным ли­нейным отрезкам соответствуют равные значения логарифмов чисел. Такой подход имеет преимущество: возможность уменьшения разме­ров больших чисел через их логарифмические эквиваленты. Однако с масштабной шкалой в виде логарифмов график малодоступен для понимания. Необходимо рядом с логарифмами, обозначенными на масштабной шкале, проставить сами числа, характеризующие уров­ни изображаемого ряда динамики, которые соответствуют указанным числам логарифмов. Такого рода графики носят название графиков на полулогарифмической сетке.

Динамику изображают и радиальные диаграммы, строящиеся в полярных координатах. Радиальные диаграммы преследуют цель на­глядного изображения определенного ритмического движения во вре­мени. Чаще всего эти диаграммы применяются для иллюстрации се­зонных колебаний. Радиальные диаграммы разделяются на замкнутые и спиральные. По технике построения радиальные диаграммы отли­чаются друг от друга в зависимости от того, что взято в качестве пун­кта отсчета - центр круга или окружность.

Замкнутые диаграммы отражают внутригодичный цикл динами­ки какого-либо одного года. Спиральные диаграммы показывают внут­ригодичный цикл динамики за ряд лет (рис. 5.11).

Построение замкнутых диаграмм сводится к следующему: вычер­чивается круг, среднемесячный показатель приравнивается к радиусу этого круга. Затем весь круг делится на 12 радиусов, которые на графи­ке приводятся в виде тонких линий. Каждый радиус обозначает месяц, причем расположение месяцев аналогично циферблату часов: январь - в том месте, где на часах 1, февраль - 2 и т.д. На каждом радиусе дела­ется отметка в определенном месте согласно масштабу исходя из дан­ных за соответствующий месяц. Если данные превышают среднеме­сячный уровень, отметка делается за пределами окружности на продолжении радиуса. Затем отметки различных месяцев соединяют­ся отрезками. В приведенном примере (рис. 11) К = 44,8 тыс. т, длина радиуса - 3,0 см. Следовательно, 1 см = 44,8 : 3,0 = 15 тыс. т. Данная замкнутая диаграмма наглядно показывает, что производство мяса под­вергнуто сезонным колебаниям.

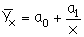
Рис. 5.11.

Минимум производства мяса прихо­дится на апрель, май, затем наблюдается медленное его повышение к августу, резкий подъем в сентябре, октябре и опять спад в декабре, ян­варе. Если же в качестве базы для отсчета взять не центр круга, а ок­ружность, то диаграммы называются спиральными.

Построение спиральных диаграмм отличается от замкнутых тем, что в них декабрь одного года соединяется не с январем данного же года, а с январем следующего года. Это дает возможность изобразить весь ряд динамики в виде спирали. Особенно наглядна такая диаг­рамма, когда наряду с сезонными изменениями происходит неуклон­ный рост из года в год (рис. 5.12).

Рис. 5.12.

5.6. Статистические карты

Статистические карты представляют собой вид графических изображений статистических данных на схематической географичес­кой карте и характеризуют уровень или степень распространения того или иного явления на определенной территории.

Средствами изображения территориального размещения являют­ся штриховка, фоновая раскраска или геометрические фигуры. Раз­личают картограммы и картодиаграммы.

Картограмма - это схематическая географическая карта, на кото­рой штриховкой различной густоты, точками или окраской определен­ной степени насыщенности показывается сравнительная интенсивность какого-либо показателя в пределах каждой единицы нанесенного на кар­ту территориального деления (например, плотность населения по облас­тям или республикам, распределение районов по урожайности зерно­вых культур и т.п.). Картограммы делятся на фоновые и точечные

Картограмма фоновая - вид картограммы, на которой штрихов­кой различной густоты или окраской определенной степени насыщен­ности показывают интенсивность какого-либо показателя в пределах территориальной единицы.

Картограмма точечная - вид картограммы, где уровень выбран­ного явления изображается с помощью точек. Точка изображает одну единицу совокупности или некоторое их количество, показывая на географической карте плотность или частоту проявления определен­ного признака.

Фоновые картограммы, как правило, используются для изображе­ния средних или относительных показателей, точечные - для объем­ных (количественных) показателей (численность населения, поголовье скота и т.д.).

Среди картодиаграмм следует выделить картодиаграммы просто­го сравнения, графики пространственных перемещений, изолинии (рис. 5.13).

 

Рис. 5.13. Плотность населения в областях Центрального района России

На картодиаграмме простого сравнения в отличие от обычной диаграммы диаграммные фигуры, изображающие величины иссле­дуемого показателя, расположены не в ряд, как на обычной диаграм­ме, а разносятся по всей карте в соответствии с тем районом, облас­тью или страной, которые они представляют.

Элементы простейшей картодиаграммы можно обнаружить на политической карте, где города отличаются различными геометричес­кими фигурами в зависимости от числа жителей.

Изолинии (греч. Isos –равный, одинаковый, подобный) – это линии равного значения какой-либо величины в ее распространении на по­верхности, в частности на географической карте или графике. Изолиния отражает непрерывное изменение исследуемой величины в зависимости от двух других переменных и применяется при картографиро­вании природных и социально-экономических явлений. Изолинии ис­пользуются для получения количественных характеристик исследуемых величин и для анализа корреляционных связей между ними.

Перечисленные виды графиков не являются исчерпывающими, но они наиболее часто употребляемы.

ОСНОВНЫЕ ПОНЯТИЯ

Абсцисса (ось х) – горизонтальная ось графика. На ней отклады­ваются значения независимой переменной или времени, или значе­ния признака.

Графический образ – совокупность точек, линий, фигур, с помо­щью которых изображаются статистические показатели.

Диаграммы динамики – линейные, спиральные, радиальные, квадратные, круговые, ленточные, фигур-знаков, секторные.

Диаграммы сравнения – столбиковые, ленточные, направлен­ные, квадратные, круговые, фигур-знаков.

Картограмма – на схематическую географическую карту нано­сится штриховка различной частоты, точки или окраска определен­ной насыщенности, которая показывает сравнительную интенсивность какого-либо показателя в пределах каждой единицы нанесенного на карту территориального деления.

Картодиаграмма представляет собой сочетание диаграмм с гео­графической картой,

Координаты линейной диаграммы – оси х и у графика.

Масштабная шкала – линия, отдельные точки которой могут быть прочитаны как определенные числа (прямолинейная или криво­линейная).

Масштабные ориентиры – масштаб и система масш… Продолжение »