6. Статистическое изучение взаимосвязи социально-экономических явлений

6.1. Причинность, регрессия, корреляция

Исследование объективно существующих связей между явления­ми - важнейшая задача общей теории статистики. В процессе статистического исследования зависимостей вскрываются причинно-след­ственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие существенное влияние на вариа­цию изучаемых явлений и процессов. Причинно-следственные от­ношения - это связь явлений и процессов, при которой изменение одного из них - причины - ведет к изменению другого - следствия.

Причина - это совокупность условий, обстоятельств, действие которых приводит к появлению следствия. Если между явлениями действительно существуют причинно-следственные отношения, то эти условия должны обязательно реализовываться вместе с действием причин. Причинные связи носят всеобщий и многообразный харак­тер, и для обнаружения причинно-следственных связей необходимо отбирать отдельные явления и изучать их изолированно.

Особое значение при исследовании причинно-следственных свя­зей имеет выявление временной последовательности: причина всегда должна предшествовать следствию, однако не каждое предшествую­щее событие следует считать причиной, а последующее - следствием.

В реальной социально-экономической действительности причину и следствие необходимо рассматривать как смежные явления, появле­ние которых обусловлено комплексом сопутствующих более простых причин и следствий. Между сложными группами причин и следствий возможны многозначные связи, в которых за одной причиной будет сле­довать то одно, то другое действие или одно действие будет иметь не­сколько различных причин. Чтобы установить однозначную причин­ную связь между явлениями или предсказать возможные следствия конкретной причины, необходима полная абстракция от всех прочих явлений в исследуемой временной или пространственной среде. Тео­ретически такая абстракция воспроизводится. Приемы абстракции ча­сто применяются при изучении взаимосвязей между двумя признаками (парная корреляция). Но чем сложнее изучаемые явления, тем труднее выявить причинно-следственные связи между ними. Взаимное пере­плетение различных внутренних и внешних факторов неизбежно при­водит к некоторым ошибкам в определении причины и следствия.

Особенностью причинно-следственных связей в социально-эко­номических явлениях является их транзитивность, т.е. причина X и следствие У связаны соотношением 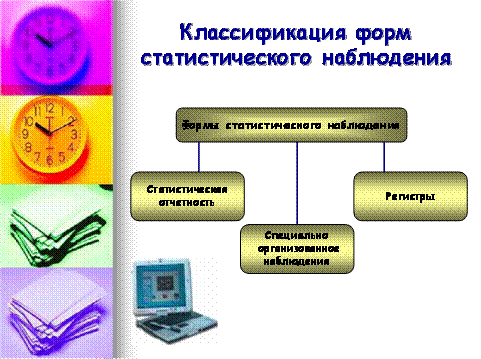, а не непосред­ственно .

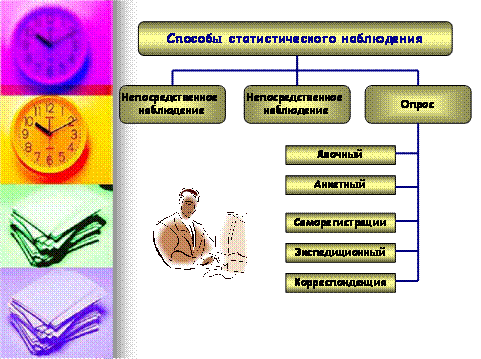Однако промежуточные факторы, как правило, при анализе опускаются.

Так, например, при использовании показателей международной методологии расчетов фактором валовой прибыли (У) считается ва­ловое накопление основных и оборотных фондов (X), но при этом допускаются такие факторы, как валовой выпуск (Х^/), оплата труда (X") и т. д. Правильно вскрытые причинно-следственные связи позволяют установить силу воздействия отдельных факторов на резуль­таты хозяйственной деятельности.

Социально-экономические явления представляют собой резуль­тат одновременного воздействия большого числа причин. Следова­тельно, при изучении этих явлений необходимо, абстрагируясь от вто­ростепенных, выявлять главные, основные причины.

На первом этапе статистического изучения связи осуществляет­ся качественный анализ изучаемого явления методами экономичес­кой теории, социологии, конкретной экономики.

На втором этапе строится модель связи на основе методов ста­тистики: группировок, средних величин, таблиц и т. д.

На третьем, последнем этапе интерпретируются результаты; анализ вновь связан с качественными особенностями изучаемого яв­ления.

Статистика разработала множество методов изучения связей, вы­бор которых зависит от целей исследования и поставленных задач. Связи между признаками и явлениями, ввиду их большого разнооб­разия, классифицируются по ряду оснований. Признаки по значению для изучения взаимосвязи делятся на два класса. Признаки, обуслав­ливающие изменения других, связанных с ними признаков, называ­ются факторными, или просто факторами. Признаки, изменяющие­ся под действием факторных признаков, являются результативными. Связи между явлениями и их признаками классифицируются по сте­пени тесноты связи, направлению и аналитическому выражению.

В статистике различают функциональную связь и стохастическую зависимость. Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Функциональная связь проявляется во всех случаях наблюдения и для каждой конкрет­ной единицы исследуемой совокупности.

Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохас­тической является корреляционная связь, при которой изменение сред­него значения результативного признака обусловлено изменением факторных признаков.

По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. Так, например, рост производительности труда способствует увеличению уровня рентабельности производства. В случае обратной связи значе­ния результативного признака изменяются под воздействием фактор­ного, но в противоположном направлении по сравнению с изменением факторного признака. Так, с увеличением уровня фондоотдачи снижа­ется себестоимость единицы производимой продукции.

По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные. Если статистическая связь меж­ду явлениями может быть приближенно выражена уравнением прямой линии, то ее называют линейной связью; если же она выражается уравнением какой-либо кривой линии (параболы, гиперболы, степен­ной, показательной, экспоненциальной и т. д.), то такую связь назы­вают нелинейной, или криволинейной.

В статистике не всегда требуются количественные оценки связи, ча­сто важно определить лишь ее направление и характер, выявить форму воздействия одних факторов на другие. Для выявления наличия связи, ее характера и направления в статистике используются методы приведе­ния параллельных данных; аналитических группировок; графический, корреляционный, регрессионный.

Метод приведения параллельных данных основан на сопоставле­нии двух или нескольких рядов статистических величин. Такое сопо­ставление позволяет установить наличие связи и получить представ­ление о ее характере. Сравним изменения двух величин X и У. С увеличением величины X величина У также возрастает. Поэтому связь между ними прямая, и описать ее можно или уравнением прямой, или уравнением параболы второго порядка.

 

Взаимосвязь двух признаков изображается графически с помощью поля корреляции. В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат –результативного.  Каждое пересечение линий, проводимых через эти оси, обозначается точкой. При отсутствии тесных связей наблюдается беспорядочное рас­положение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи (рис. 6.1).

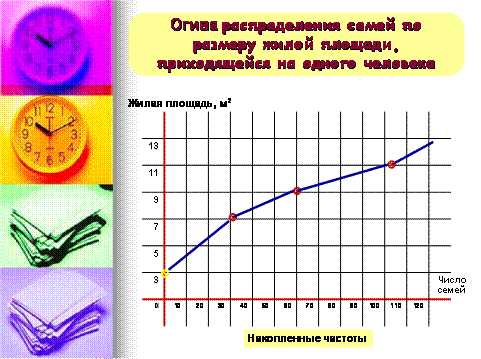
Рис. 6.1.

 Для социально-экономических явлений характерно, что наряду с существенными факторами, формирующими уровень результативно­го признака, на него оказывают воздействие многие другие неучтен­ные и случайные факторы. Это свидетельствует о том, что взаимосвя­зи явлений, которые изучает статистика, носят корреляционный характер и аналитически выражаются функцией вида .

Корреляционный метод имеет своей задачей количественное оп­ределение тесноты связи между двумя признаками (при парной свя­зи) и между результативным и множеством факторных признаков (при многофакторной связи).

Корреляция - это статистическая зависимость между случайны­ми величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к из­менению математического ожидания другой.

В статистике различаются следующие варианты зависимостей:

• парная корреляция - связь между двумя признаками (результа­тивным и факторным или двумя факторными);
• частная корреляция - зависимость между результативным и одним факторным признаками при фиксированном значении дру­гих факторных признаков;
• множественная корреляция - зависимость результативного и двух или более факторных признаков, включенных в исследование.

Теснота связи количественно выражается величиной коэффици­ентов корреляции. Коэффициенты корреляции, представляя количе­ственную характеристику тесноты связи между признаками, дают возможность определить «полезность» факторных признаков при по­строении уравнений множественной регрессии. Величина коэффици­ента корреляции служит также оценкой соответствия уравнения рег­рессии выявленным причинно-следственным связям.

Первоначально исследования корреляции проводились в биологии, а позднее распространились и на другие области, в том числе на соци­ально-экономическую. Одновременно с корреляцией начала использо­ваться и регрессия. Корреляция и регрессия тесно связаны между собой: корреляция оценивает силу (тесноту) статистической связи, регрессия исследует ее форму. Та и другая служат для установления соотношения между явлениями, для определения наличия или отсутствия связи.

Корреляционный и регрессионный анализ как общее понятие вклю­чает в себя измерение тесноты, направления связи и установление ана­литического выражения (формы) связи (регрессионный анализ).

Регрессионный метод заключается в определении аналитическо­го выражения связи, в котором изменение одной величины (называе­мой зависимой или результативным признаком) обусловлено влияни­ем одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значе­ния. Регрессия может быть однофакторной (парной) и многофактор­ной (множественной).

По форме зависимости различают:

линейную регрессию, которая выражается уравнением прямой (линейной функцией) вида:

нелинейную регрессию, которая выражается уравнениями вида:

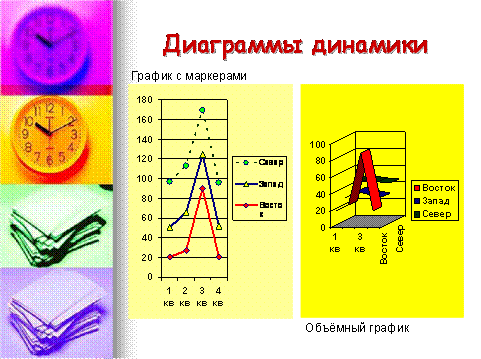парабола;

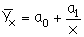гипербола и т.д.

По направлению связи различают:

• прямую регрессию (положительную), возникающую при условии, если с увеличением или уменьшением независимой величины значения зависимой также соответственно увеличиваются или уменьшаются;
• обратную (отрицательную) регрессию, появляющуюся при условии, что с увеличением или уменьшением независимой величины зависимая соответственно уменьшается или увеличивается.

Положительную и отрицательную регрессии можно легче понять, если использовать их графическое изображение (см. рис. 6.1).

Для простой (парной) регрессии в условиях, когда достаточно полно установлены причинно-следственные связи, приобретает прак­тический смысл только последнее положение; при множественности причинных связей невозможно четко отграничить одни причинные явления от других.

 

6.2. Основные задачи и предпосылки применения корреляционно-регрессионного анализа

Все явления и процессы, характеризующие социально-экономи­ческое развитие и составляющие единую систему национальных сче­тов, тесно взаимосвязаны и взаимозависимы между собой.

Корреляционная зависимость является частным случаем стохас­тической зависимости, при которой изменение значений факторных признаков влечет за собой изменение среднего значения результативного признака.

Корреляционная зависимость исследуется с помощью методов корреляционного и регрессионного анализов.

Корреляционный анализ изучает взаимосвязи показателей и по­зволяет оценить:

• тесноту связи между показателями с помощью парных, част­ных и множественных коэффициентов корреляции,
• уравнение регрессии.Основной предпосылкой применения корреляционного анализа является необходимость подчинения совокупности значений всех фак­торныхи результативного (У) признаков к -мерному нор­мальному закону распределения или близость к нему. Если объем ис­следуемой совокупности достаточно большой (n > 50), то нормальность распределения может быть подтверждена на основе расчета и анализа критериев Пирсона, Ястремского, Боярского, Колмогорова, чисел Вастергарда и т. д. Если n < 50, то закон распределения исходных дан­ных определяется на базе построения и визуального анализа поля кор­реляции. При этом если в расположении точек наблюдается линейная тенденция, то можно предположить, что совокупность исходных дан­ных подчиняется нормальному распределению.регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака (У) от факторных.Основной предпосылкой регрессионного анализа является то, что только результативный признак (У) подчиняется нормальному закону рас­пределения, а факторные признаки могут иметь произволь­ный закон распределения. В анализе динамических рядов в качестве фак­торного признака выступает время t. При этом в регрессионном анализе заранее подразумевается наличие причинно-следственных связей меж­ду результативными факторными признаками.

Уравнение регрессии, или статистическая модель связи социаль­но-экономических явлений, выражаемая функцией

является достаточно адекватной реальному моделируемому явлению или процессу, если выполняются следующие требования к их построению:

• совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями;
• моделируемые явления должны описываться одним или несколькими уравнениями причинно-следственных связей;
• все факторные признаки должны иметь количественное (циф­ровое) выражение;
• объем исследуемой выборочной совокупности должен быть достаточно большим;
• причинно-следственные связи между явлениями и процессами должны описываться линейной или приводимой к линейной формами зависимости,
• параметры модели связи не должны иметь количественных ограничений,
• территориальная и временная структура изучаемой совокупности должна быть постоянной.

Соблюдение данных требований позволяет исследователю постро­ить статистическую модель связи, наилучшим образом аппроксимиру­ющую моделируемые социально-экономические явления и процессы

Теоретическая обоснованность моделей взаимосвязи, построен­ных на основе корреляционно-регрессионного анализа, обеспечива­ется соблюдением следующих основных условий.

• все признаки и их совместные распределения должны подчиняться нормальному закону распределения;
• в дисперсия моделируемого признака (У) должна все время оста­ваться постоянной при изменении величины (У) и значений фак­торных признаков;
• отдельные наблюдения должны быть независимыми, т. е резуль­таты, полученные в i-м наблюдении, не должны быть связаны с предыдущими и содержать информацию о последующих наблю­дениях, а также влиять на них.

Отступление от выполнения этих условий и предпосылок приво­дит к тому, что модель регрессии будет неадекватно отражать реаль­но существующие связи между анализируемыми признаками

Одной из проблем построения уравнения регрессии является ее размерность, т е определение числа факторных признаков, включа­емых в модель Их число должно быть оптимальным.

Сокращение размерности за счет исключения второстепенных, несущественных факторов позволяет получить модель, реализуемую быстрее и качественнее. В то же время построение модели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление или процесс в единой системе наци­онального счетоводства.

Практика выработала определенный критерий, позволяющий ус­тановить оптимальное соотношение между числом факторных при­знаков, включаемых в модель, и объемом исследуемой совокупнос­ти. Согласно данному критерию, число факторных признаков (k) должно быть в 5-6 раз меньше объема изучаемой совокупности.

Общая блок-схема реализации корреляционного и регрессионно­го методов анализа представлена на рис. 6.2.

Приведенная последовательность реализации корреляционного и регрессионного методов анализа позволяет достаточно полно охарак­теризовать и смоделировать реально существующие взаимосвязи и взаимозависимости между показателями, характеризующими разви­тие социально-экономических явлений и процессов.

 

Рис. 6.2.

Построение корреляционно-регрессионных моделей, какими бы сложными они ни были, само по себе не вскрывает полностью всех при­чинно-следственных связей. Основой их адекватности является предва­рительный качественный анализ, основанный на учете специфики и осо­бенностей исследуемых социально-экономических явлений и процессов.

 

 

6.3. Парная регрессия на основе метода наименьших квадратов и метода группировок

Парная регрессия характеризует связь между двумя признаками - результативным и факторным. Аналитическая связь между ними опи­сывается следующими уравнениями:

 прямой

гиперболы

  параболы и т.д.

 

Определить тип уравнения можно, исследуя зависимость графи­чески. Однако существуют более общие указания, позволяющие выя­вить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, при­мерно в арифметической прогрессии, то это свидетельствует о том, что связь между ними линейная, а при обратной связи - гиперболи­ческая. Если факторный признак увеличивается в арифметической прогрессии, а результативный - значительно быстрее, то использует­ся связь параболическая или степенная.

Оценка параметров уравнений регрессии (а₀, а₁, и а₂ в уравнении параболы второго порядка) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности.

Основной принцип метода наименьших квадратов рассмотрим на следующем примере: будем считать, что две величины (два пока­зателя) X и У взаимосвязаны между собой, причем У находится в не­которой зависимости от Х. Следовательно, У будет зависимой, а Х- независимой величинами.

 

Сущность метода наименьших квадратов заключается в нахожде­нии параметров модели (а₀, а₁), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений резуль­тативного признака от теоретических, полученных по выбранному уравнению регрессии:  

Для прямой зависимости:

 

• Рассмотрим S в качестве функции параметров а₀ и а₁, проведем математические преобразования (дифференцирование) и получим:

  Откуда система нормальных уравнений для нахождения парамет­ров линейной парной регрессии методом наименьших квадратов при­мет следующий вид:

  

  где n - объем исследуемой совокупности (число единиц наблюдений).

  В уравнениях регрессии параметр а₀ показывает усредненное вли­яние на результативный признак неучтенных (не выделенных для ис­следования) факторов; параметр а₁ (а в уравнении параболы и а₂) –коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.

  Применение метода наименьших квадратов объясняется неизбеж­ным наличием случайных ошибок в результатах опыта.

  Статистические данные обладают ошибками упрощения, кото­рые возникают как следствие:

  неполноты охвата, потому что часть единиц совокупности, полученных в результате наблюдения, не может быть использована в исследовании;

  неполноты факторов, определяющих то или иное социально-эко­номическое явление, в силу того, что ни в одно уравнение, или модель, нельзя включить бесконечное число аргументов (во всех случаях отбирается только часть воздействующих факторов, причем отбор носит чисто субъективный характер);

  характера выбранного уравнения связи. Как бы хорошо оно ни было обосновано, как бы теоретически адекватно ни описыва­ло исследуемое явление, оно не может быть его точным аналогом.

  Решение вопроса о возможности использования метода наимень­ших квадратов для изучения связей между социально-экономически­ми явлениями зависит от свойства оценок, получаемых с помощью этого метода.

  Даже при сравнительно небольшом числе наблюдений примене­ние метода наименьших квадратов позволяет получить достоверные оценки.

  Метод наименьших квадратов может быть также использован в анализе косвенных наблюдений, являющихся функциями многих не­известных.

  Обобщенная блок-схема построения уравнения парной регрессии представлена на рис. 6.3.

  Рис. 6.3.

   

  6.4. Множественная (многофакторная) регрессия

  Изучение связи между тремя и более связанными между собой признаками носит название множественной (многофакторной) рег­рессии. При исследовании зависимостей методами множественной регрессии задача формулируется так же, как и при использовании парной регрессии, т.е. требуется определить аналитическое выражение связи между результативным признаком и факторными при­знаками,найти функцию:

Построение моделей множественной регрессии включает несколько этапов:

• выбор формы связи (уравнения регрессии);
• отбор факторных признаков;
• обеспечение достаточного объема совокупности для получения несмещенных оценок.

Рассмотрим каждый из них.

Выбор формы связи затрудняется тем, что с использованием ма­тематического аппарата теоретически зависимость между признака­ми выражается большим числом различных функций.

Выбор типа уравнения осложнен тем, что для любой формы зави­симости выбирается целый ряд уравнений, которые в определенной степени будут описывать эти связи. Некоторые предпосылки для вы­бора определенного уравнения регрессии получают на основе анали­за предшествующих аналогичных исследований или на базе анализа подобных работ в смежных отраслях знаний. Поскольку уравнение регрессии строится главным образом для объяснения и количествен­ного выражения взаимосвязей, оно должно хорошо отражать сложив­шиеся между исследуемыми факторами фактические связи.

Наиболее приемлемым способом определения вида исходного уравнения регрессии является метод перебора различных уравнений.

Сущность данного метода заключается в том, что большое число уравнений (моделей) регрессии, отобранных для описания связей ка­кого-либо социально-экономического явления или процесса, реализу­ется на ЭВМ с помощью специально разработанного алгоритма пере­бора с последующей статистической проверкой, главным образом, на основе - критерия Стьюдента и F -критерия Фишера-Снедекора.

Способ перебора является достаточно трудоемким и связан с боль­шим объемом вычислительных работ.

Практика построения многофакторных моделей взаимосвязи по­казывает, что все реально существующие зависимости между соци­ально-экономическими явлениями можно описать, используя пять типов моделей:

1) линейную:

2) степенную:

3) показательную:

4) параболическую:

5)         гиперболическую

Основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации. Нелинейные формы зависимости приводятся к линейным путем линеаризации.

Важным этапом построения уже выбранного уравнения множе­ственной регрессии является отбор и последующее включение фак­торных признаков.

Сложность формирования уравнения множественной регрессии заключается в том, что почти все факторные признаки находятся в зависимости один от другого.

Определение размерности модели связи, т.е. определение оптималь­ного числа факторных признаков, является одной из основных проблем построения множественного уравнения регрессии. В то же время чем больше факторных признаков включено в уравнение, тем оно лучше описывает явление. Однако модель размерностью 100 и более фактор­ных признаков сложно реализуема и требует больших затрат машинного времени. Сокращение размерности модели за счет исключения второ­степенных, экономически и статистически несущественных факторов способствует простоте и качеству ее реализации. Но построение модели регрессии малой размерности может привести к тому, что такая модель будет недостаточно адекватна исследуемым явлениям и процессам.

Проблема отбора факторных признаков для построения моде­лей взаимосвязи может быть решена на основе эвристических или многомерных статистических методов анализа.

Обобщенную методику корреляционного метода анализа экономи­ческих явлений и процессов можно представить блок-схемой (рис. 6.4.).

 

Рис. 6.4.

 

6.5. Методы изучения связи социальных явлений

Важной задачей статистики является разработка методики стати­стической оценки социальных явлений, которая осложняется тем, что многие социальные явления не имеют количественной оценки.

Как правило, анализ социальных явлений, их связей и зависимос­тей должен начинаться с построения графиков связей. В настоящее время используются графики, характеризующие связь социальных явлений (рис. 6.5.).

С помощью графика (рис. 6.5,а) «цепь» изображаются связи между социальными признаками, которые одинаково существенны и значимы.

График (рис. 6.7,б) «звезда» изображает зависимость социальных явлений, которые тяготеют к одному наиболее значимому. Исключе­ние данного признака нарушает взаимосвязи между оставшимися при­знаками.

На графике (рис. 6.5,в) «сетка» выделяется несколько значимых признаков, которые тесно зависимы друг от друга.

Для количественной характеристики многомерных (многофакторных) связей социальных явлений используется метод корреляционны плеяд, основанный на расчете коэффициентов связи, которые носят об­щее название информативных коэффициентов.… Продолжение »